In the vast realm of naval architecture, the concept of metacentric height stands as a cornerstone. It’s a term that, while perhaps unfamiliar to many, plays a pivotal role in ensuring the stability and safety of ships.
Today, I’ll be sharing insights into the intriguing world of metacentric height, its calculation, and the factors that influence it.
We’ll delve into its critical role in ship stability, how it impacts ship design, and even explore real-world applications.
This exploration will not only demystify the concept but also underscore its importance in naval architecture. So, whether you’re a maritime enthusiast or a professional in the field, this comprehensive guide on metacentric height promises to be an enlightening read.

Understanding Metacentric Height
Definition of Metacentric Height
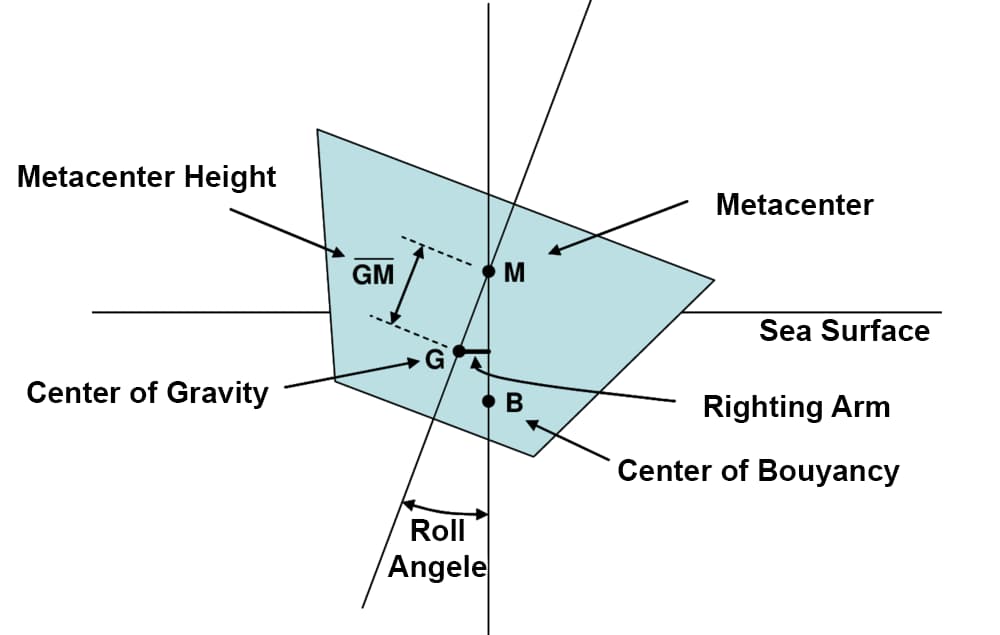
Metacentric height, often denoted as GM, is a measure of the initial static stability of a floating body, such as a ship. It is calculated as the distance between the center of gravity (G) of the ship and its metacenter (M).
The metacenter is the point about which a floating body starts oscillating when given a small angular displacement. A larger metacentric height implies greater initial stability against overturning.
Calculation of Metacentric Height
Calculating the metacentric height involves determining the distance between a ship’s center of gravity and its metacenter. As mentioned above, metacentric height measurement is represented as GM, where G represents the center of gravity and M represents the metacenter.
The formula for calculating metacentric height is GM = KM – KG, where KM is the distance from the keel to the metacenter and KG is the distance from the keel to the center of gravity.
Here are major scenarios of different metacentric height values: negative, positive, zero, and excessive metacentric heights.
Positive Metacentric Height (GM)
A positive GM signifies that the metacenter is above the center of gravity. This is generally desirable for most seafaring vessels because it allows for increased initial stability.
In this scenario, when a ship tilts or heels due to external forces such as wind or waves, the buoyancy force’s line of action changes to act through a point further from the centerline (the metacenter), creating a righting moment that attempts to return the ship to its upright position. This is analogous to a pendulum, which always tries to return to the vertical position due to gravity.
For instance, oil tankers and cargo ships are usually designed with a high GM to prevent capsizing in rough sea conditions.
Negative Metacentric Height (GM)
When the GM is negative, it means the metacenter is below the center of gravity. This situation is generally undesirable because it signifies that the ship has poor initial stability.
In this case, when the ship heels, the buoyancy force’s line of action falls to the same side as the tilt, further accentuating the tilt rather than correcting it. This can lead to the risk of capsizing.
A real-life example can be found in improperly loaded cargo ships. If too much weight is placed high up in the ship, it can raise the center of gravity and result in a negative GM.
Zero Metacentric Height (GM)
When the GM is zero, it means that the metacenter and the center of gravity are at the same height. While the ship might initially seem stable (it does not incline either way), it actually has no initial stability to resist any angular displacements.
An example might be a very flat-bottomed barge. Its low center of gravity and high center of buoyancy may coincide, resulting in a zero GM. However, any small disturbances such as wind, waves, or shifts in cargo might cause it to start tilting with nothing to bring it back to the upright position.
High Metacentric Height (GM)
While a positive GM is typically beneficial, an excessively high metacentric height can also be problematic. This could happen if the center of gravity is very low in the ship, causing a large distance to the metacenter.
In this case, the ship will have a strong righting moment and therefore a rapid, potentially uncomfortable, and dangerous roll period. This situation can be particularly problematic for passengers or cruise ships, where passenger comfort is essential. A ship with a high GM will be very stiff, leading to rapid, sharp movements in response to external forces.
This condition might occur in a ship that is underloaded or has its cargo unevenly distributed, with most of the weight concentrated at the bottom.
In all situations, proper balance and cargo distribution are key to maintaining an appropriate and safe metacentric height for the conditions the ship will encounter. It is also important to remember that while the GM can provide a good indication of initial stability, other factors such as hull shape and distribution of weight also significantly contribute to overall ship stability.
Factors Affecting Metacentric Height
Several factors can influence the metacentric height of a ship. One of the primary factors is the position of the center of gravity. If the center of gravity is too high, the metacentric height can become negative, which can affect the ship’s stability.
Another factor is the shape and size of the ship, which can affect the position of the metacenter. Additionally, external factors such as wave conditions can cause variations in the effective metacentric height. Understanding these factors is crucial for maintaining the stability of a ship.
Role of Metacentric Height in Ship Stability
The metacentric height plays a significant role in ship stability. It influences various aspects, including the righting moment, equilibrium, and ship roll. Let’s explore these relationships further.
Metacentric Height and Righting Moment
The righting moment of a ship is the torque that brings a tilted ship back to its upright position. It’s the product of the ship’s weight and the horizontal distance between the center of gravity and the center of buoyancy, known as the righting arm or lever.
The metacentric height directly influences this righting moment. A larger metacentric height means a larger righting arm, leading to a greater righting moment. This results in a ship that is more resistant to overturning, enhancing its overall stability.
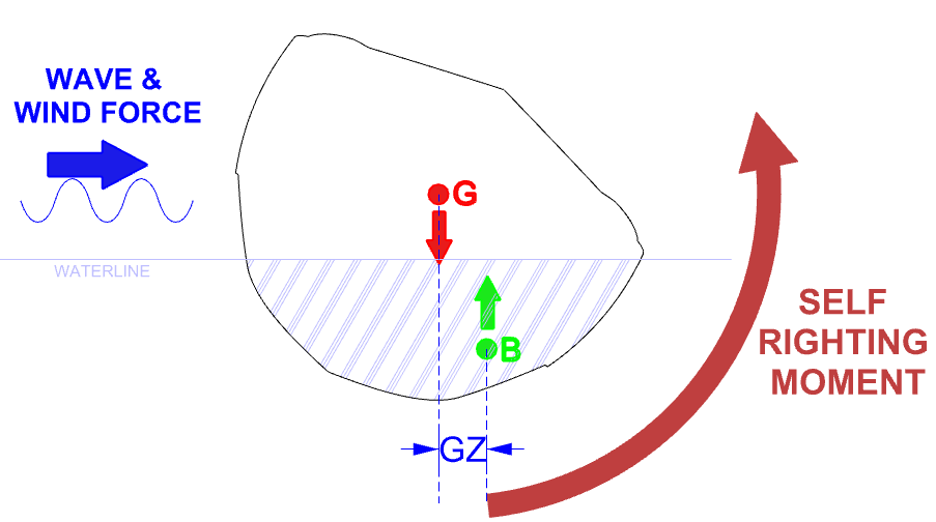
In a previous article, we discussed the concept of self-righting boats, a clear illustration of the principle of metacentric height and righting moment in action. These boats are specifically designed to return to an upright position after being significantly tilted or even capsized, thanks to their optimized center of gravity and buoyancy.
Metacentric Height and Equilibrium
Equilibrium in a ship is a state where the forces and moments acting upon it balance each other out. The metacentric height plays a crucial role in determining the type of equilibrium. If the metacentric height is positive, meaning the metacenter is above the center of gravity, the ship is in stable equilibrium.
This means that if the ship is tilted, it will return to its upright position. If the metacentric height is zero, the ship is in neutral equilibrium and will stay at the angle it’s tilted to. If the metacentric height is negative, the ship is in unstable equilibrium, and any tilt could potentially lead to capsizing.
Metacentric Height and Ship Roll
Ship roll is the oscillation of a ship about its longitudinal axis. The metacentric height has a direct impact on the ship’s roll. A larger metacentric height leads to a stiffer ship that resists roll and has a shorter roll period.
Conversely, a smaller metacentric height results in a tender ship that rolls more easily and has a longer roll period. Understanding the relationship between metacentric height and ship roll is essential for designing ships that can withstand various sea conditions.
Metacentric Height and Ship Design
Influence of Metacentric Height on Ship Design
The metacentric height is a vital parameter in ship design, influencing the ship’s stability and response to external forces.
A larger metacentric height results in a stiffer ship that resists roll and has a shorter roll period. Conversely, a smaller metacentric height leads to a tender ship that rolls more easily and has a longer roll period.
Therefore, naval architects must carefully consider the desired metacentric height when designing a ship, as it directly impacts the ship’s performance and safety at sea.
Balancing Stability and Ship Roll in Design
One of the challenges in ship design is balancing stability and ship roll. A ship with a large metacentric height will have a high initial stability and resist roll, but it will also have a short roll period, which can lead to a rough ride in heavy seas.
On the other hand, a ship with a small metacentric height will roll more easily and have a longer roll period, providing a smoother ride but at the risk of reduced stability.
Therefore, naval architects must strike a balance between stability and ship roll in their designs, taking into account the intended use of the ship and the conditions it will face. The metacentric height plays a crucial role in achieving this balance.
Real-World Examples and Applications
The principles of metacentric height are not just theoretical; they have practical applications in the real world. Let’s explore some of these applications.
Case Studies of Metacentric Height in Ships
In real-world scenarios, the metacentric height plays a crucial role in ship stability. For instance, consider the case of a cargo ship. When the ship is fully loaded, the center of gravity shifts, affecting the metacentric height.
If the metacentric height is not sufficient, the ship could become unstable, leading to potential capsizing. On the other hand, passenger ships are designed with a high metacentric height to ensure stability, even in rough seas.
However, a very high metacentric height can lead to excessive stiffness, causing discomfort due to excessive rolling. These examples underscore the importance of considering metacentric height in ship design and operation.
The Inclining Experiment
The inclining experiment is a practical method used to determine the metacentric height of a ship.
The experiment involves causing the ship to heel to small angles by moving known weights across the deck and observing the angles of inclination. The draughts of the ship are noted along with the water density.
This experiment is typically conducted on new ships or those that have undergone significant structural alterations. The data obtained from the inclining experiment is used to calculate the metacentric height, providing valuable information for assessing the ship’s stability.
Conclusion
In the realm of naval architecture, the metacentric height stands as a pivotal concept, influencing ship stability, design, and safety. From understanding its definition and calculation to exploring its role in ship stability and design, we’ve navigated the depths of this principle.
We’ve seen how it impacts the righting moment, equilibrium, and ship roll, and how it’s considered in ship design. Real-world applications, such as the inclining experiment, further underscore its practical importance.
This exploration of metacentric height illuminates its crucial role in naval architecture, providing a foundation for further study and application in the field. As we continue to advance in ship design and technology, the principles of metacentric height will remain a guiding beacon, ensuring our vessels navigate the seas with stability and safety.
- Types of Gas Carriers as per IGC Code – April 22, 2025
- Wind-Assisted Propulsion Systems (WAPS): A Game Changer for Maritime Decarbonization – February 6, 2025
- 10 Boat Salvage Yards in California – January 25, 2025




